L'accelerazione di Coriolis
Le forze apparenti o fittizie
La pagina sul pendolo di Foucault ha sollevato alcune obbiezioni sulle ragioni per le quali il piano del pendolo
ruota o sul perché gli oggetti che cadono, si spostano verso Est.
In effetti poco ho scritto sulle ragioni di tale spostamento a vantaggio della descrizione degli effetti. In
questa pagina tenterò di dare una spiegazione al perché ciò accade.
Quando siamo su una giostra, se lasciamo cadere una palla, non ci sorprende molto di vederla rotolare verso il
bordo della giostra lungo una traiettoria che non è affatto rettilinea, analogamente se l'appoggio sul piano
della giostra tenendola ferma con la mano, quando la lascio andare mi aspetto che si metta in moto.
Al contrario se la lascio cadere sul pavimento di una stanza, mi aspetto di vederla procedere lungo una retta.
Se la tengo ferma a terra con una mano, quando la lascio andare mi aspetto che rimanga immobile.
Che differenza c'è tra la giostra e la stanza?
La risposta è meno immediata di quanto può sembrare. Quando parlo della stanza, assumo implicitamente di essere
in un sistema di riferimento inerziale ovvero parto dal presupposto che gli oggetti nella stanza non siano
soggetti a forze che ne modifichino il moto. Questo naturalmente non è vero, basti pensare alla forza di gravità
ma se considero il moto sul pavimento, dato che questo mi oppone una forza normale uguale e contraria alla
forza peso, apparentemente posso dire di essere in un sistema di riferimento inerziale. Devo però dimenticare di
essere sulla Terra, che gira intorno al proprio asse, intorno al Sole, intorno al centro galattico...
Come ne esco da questo giro? Facile, il moto della mia palla dentro la stanza è influenzata da forze che hanno
effetti maggiori rispetto a quelli dovuti ai vari moti terrestri esse sono la forza di gravità e l'attrito.
È per questo motivo che sono stati necessari millenni prima che l'uomo trovasse un esperimento decisivo che
mostrasse senza dubbio il moto della Terra.
Torniamo ora al moto della palla sulla giostra.
Supponiamo di avere due osservatori, uno sulla giostra e l'altro a terra che chiamerò rispettivamente O'
ed O. Descriviamo il moto di un osservatore rispetto all'altro:
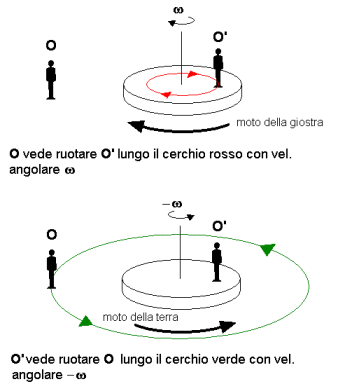
- O dirà a O' "Tu stai ruotando insieme alla giostra" come si vede in figura e misurerà una velocità angolare
 (la velocità angolare è la velocità alla quale ruota la giostra).
(la velocità angolare è la velocità alla quale ruota la giostra).
- O' dirà ad O "Non sono io a ruotare, io vedo ruotare tu e tutta la terra a velocità angolare -
 ".
".
Quale dei due osservatori ha ragione? Ha ragione colui che dimostra di essere su un sistema di riferimento inerziale.
Vediamo ora alcune relazioni e poi torniamo ai nostri due osservatori.
Consideriamo un oggetto sulla giostra, ad esempio un cavallino. La sua velocità V misurata da terra, è
data dalla velocità angolare moltiplicata per la distanza r dal centro della giostra.
La velocità misurata sulla giostra è zero.
Scriviamo la relazione in termini rigorosi:
V =  x r (eq.1)
x r (eq.1)
Naturalmente V,  ed r sono vettori e x è il prodotto vettore.
Se l'oggetto si muove anche sulla giostra, questa velocità V' si somma vettorialmente:(vedi qui somma e prodotti sui vettori)
ed r sono vettori e x è il prodotto vettore.
Se l'oggetto si muove anche sulla giostra, questa velocità V' si somma vettorialmente:(vedi qui somma e prodotti sui vettori)
V = V' +  x r (eq.2)
x r (eq.2)
Questa relazione è generale e dice che un oggetto in moto apparirà spostarsi a velocità V per l'osservatore
O e a velocità V' per l'osservatore O'.
Vediamo adesso come si trasforma l'accelerazione. L'accelerazione ci dice come varia la velocità nel tempo, infatti
accelerando o decelerando aumento o diminuisco la velocità. Formalmente devo utilizzare le derivate e per chi non le
conosce o non le ricorda consiglio di vedersele qui.
L'accelerazione di un oggetto in moto circolare uniforme è data da:
a = dV/dt =  x dr/dt =
x dr/dt =  x (
x ( x dr) (eq.3)
x dr) (eq.3)
Se il moto non è uniforme devo derivare l'eq. 3 e devo derivare anche la V' rispetto O, quindi la relazione diventa:
a = dV/dt = dV'/dt +  x dr/dt (eq.4)
x dr/dt (eq.4)
L'ultimo termine può essere semplificato facendo uso dell'eq. 2:
 x dr/dt =
x dr/dt =  x V =
x V =  x (V' +
x (V' +  x r ) =
x r ) =  x V' +
x V' +  x (
x ( x r) (eq.5)
x r) (eq.5)
Il termine dV'/dt è la derivata calcolata rispetto l'osservatore O e in generale è diversa se calcolata rispetto ad O'.
O' osserva l'oggetto muoversi con accelerazione a' e quindi devo scrivere:
dV/dt = dV'/dt +  x V' = a' +
x V' = a' +  x V' (eq.6)
x V' (eq.6)
Sostituendo l'eq. 5 e 6 nella 4 otteniamo infine:
a = a' + 2 x V' +
x V' +  x (
x ( x r) (eq.7)
x r) (eq.7)
Questa equazione ci dà la relazione tra le accelerazioni a e a' dell'oggetto rispetto agli
osservatori O e O' in moto relativo rotatotio uniforme. Il secondo termine 2 x V'
è noto con il nome di accelerazione di Coriolis (Gaspard Gustave Coriolis Parigi 1792-1843) mentre il terzo termine è l'accelerazione centripeta.
x V'
è noto con il nome di accelerazione di Coriolis (Gaspard Gustave Coriolis Parigi 1792-1843) mentre il terzo termine è l'accelerazione centripeta.
I moti relativi alla Terra
L'accelerazione di Coriolis produce effetti interessanti e inaspettati sui moti degli oggetti sulla Terra.
Adesso siamo in grado di rispondere alla domanda su quale dei due osservatori O e O' è inerziale.
È sufficiente chiedere ad O e O' di fare alcuni esperimenti e di rivelarci i risultati.
Chiediamo ad esempio di far cadere un sasso. Il sasso di O cadrà dritto verso il suolo come confermerà O, O' invece
ci dirà che il sasso non è andato giù diretto verso il suolo ma ha subito una leggera deviazione.
O è in un sistema di riferimento inerziale e O' no! Oltre alla accelerazione di Coriolis, anche
l'accelerazione centripeta produce effetti.
Vediamo cosa succede in dettaglio. Chiamiamo go l'accelerazione di gravità che si misurerebbe in un punto
A della superficie terrestre se la Terra non fosse in rotazione. go corrisponde allora ad a
dell'eq. 7. Risolvendola in funzione di a' ottengo
a' = go - 2 x V' -
x V' -  x (
x ( x r) (eq.8)
x r) (eq.8)
Se consideriamo un corpo in quiete o in moto a velocità piccola rispetto la Terra, la componente di Coriolis può
essere trascurata rispetto all'ultimo termine -  x (
x ( x r)
detto accelerazione centrifuga. L'accelerazione a' misurata in questo caso è detta accelerazione efficace
di gravità e si indica con g. Allora:
x r)
detto accelerazione centrifuga. L'accelerazione a' misurata in questo caso è detta accelerazione efficace
di gravità e si indica con g. Allora:
g = go -  x (
x ( x r) (eq.9)
x r) (eq.9)
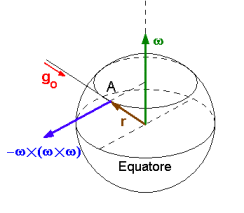 Poiché g è la somma di go e l'accelerazione centrifuga, la direzione di g è chiamata
verticale ed è determinata dalla direzione del filo a piombo. I liquidi si dispongono con la superficie perpendicolare
a g. La direzione di g non punta perfettamente verso il centro della Terra (se supponiamo che sia
una sfera perfetta) ma è spostato in base alla accelerazione in quel punto.
Poiché g è la somma di go e l'accelerazione centrifuga, la direzione di g è chiamata
verticale ed è determinata dalla direzione del filo a piombo. I liquidi si dispongono con la superficie perpendicolare
a g. La direzione di g non punta perfettamente verso il centro della Terra (se supponiamo che sia
una sfera perfetta) ma è spostato in base alla accelerazione in quel punto.
L'ordine di grandezza è:
|-  x (
x ( x r)| = 3.39 x 10-2 m s-1 (eq.10)
x r)| = 3.39 x 10-2 m s-1 (eq.10)
(dove  = 7.292 x 10-5 rad s-1 e r = 6.37 x 106 m)
e decresce andando dall'equatore verso i poli (dove è zero). Questo valore è molto piccolo rispetto alla accelerazione di gravità
tuttavia riesce a modificare il valore di g come si vede dalla tabella.
= 7.292 x 10-5 rad s-1 e r = 6.37 x 106 m)
e decresce andando dall'equatore verso i poli (dove è zero). Questo valore è molto piccolo rispetto alla accelerazione di gravità
tuttavia riesce a modificare il valore di g come si vede dalla tabella.
| Località | Latitudine | Gravità |
| Polo Nord | 90o 0' | 9.8321 |
| Anchorage | 61o 10' | 9.8218 |
| Greenwich | 51o 29' | 9.8119 |
| Parigi | 48o 50' | 9.8094 |
| Washington | 38o 53' | 9.8011 |
| Panama | 8o 55' | 9.7822 |
| Equatore | 0o 0' | 9.7799 |
L'effetto della accelerazione centrifuga su un corpo in caduta libera è un leggero spostamento della
traiettoria del corpo rispetto alla direzione radiale in direzione dell'equatore.
Consideriamo ora il termine di Coriolis - 2 x V'. Per un corpo in caduta libera
la velocità V' è diretta verticalmente verso il suolo (nella direzione del filo a piombo).
x V'. Per un corpo in caduta libera
la velocità V' è diretta verticalmente verso il suolo (nella direzione del filo a piombo).
Allora poiché  è parallela all'asse terrestre, il termine di Coriolis è diretto verso Est.
è parallela all'asse terrestre, il termine di Coriolis è diretto verso Est.
Se il moto avviene su un piano orizzontale, l'accelerazione di Coriolis provoca una deviazione dalla traiettoria
rettilinea, verso destra nell'emisfero boreale e verso sinistra in quello australe. Questo effetto aumenta vicino ai poli.
L'effetto di Coriolis, trascurabile nella maggior parte dei casi, ha un notevole effetto sui razzi e sui satelliti
a causa della loro alta velocità. Infatti mentre l'accelerazione centrifuga ha lo stesso effetto su ogni corpo
indifferentemente dalla sua velocità (nella relazione compare solo la velocità angolare e la distanza dal centro della Terra),
la accelerazione di Coriolis aumenta all'aumentare della velocità del corpo.
Vi sono alcuni fenomeni comuni che subiscono visibilmente l'effetto dell'accelerazione di Coriolis, il più evidente
è il movimento spiraleggiante dei venti che spirano verso le cellule cicloniche (basse pressioni).
L'aria infatti non si sposta lungo una retta dall'alta pressione verso la bassa pressione ma, a causa dell'accelerazione di Coriolis,
compie dei moti in senso antiorario nel nostro emisfero e in senso orario nell'emisfero australe (anche la pressione e la temperatura hanno un effetto importante sui moti, l'effetto di Coriolis è solo la causa principale del movimento spiraleggiante).
Un secondo esempio è la rotazione del piano di oscillazione di un pendolo, dimostrato in maniera spettacolare da Foucault nel 1851
come abbiamo visto nella pagina de La rotazione della Terra ed il pendolo di Foucault.
Un esercizio
Vediamo di quanto devia un corpo in caduta libera all'equatore:
l'angolo formato tra V' e  è di 90o pertanto il seno è uguale a 1.
è di 90o pertanto il seno è uguale a 1.
Il modulo dell'accelerazione di Coriolis è 2 V' pertanto posso scrivere:
V' pertanto posso scrivere:
d2x/dt2 = 2 V'
V'
V' è la velocità del corpo in caduta libera pertanto: V' = gt e la relazione precedente diventa:
d2x/dt2 = 2 gt
gt
integrando e supponendo che all'istante iniziale la velocità del corpo sia nulla ottengo:
dx/dt =  gt2
gt2
Integrando di nuovo e assumendo che per t=0 il corpo si trova esattamente sulla verticale di A con x = 0, ho:
x = 1/3  gt3
gt3
che dà lo spostamento verso est in funzione del tempo di caduta. Se il corpo cade dall'altezza h = 1/2 gt, possiamo scrivere:
x = 1/3  (8h3/g)1/2 = 1.53 x 10-5 h3/2
(8h3/g)1/2 = 1.53 x 10-5 h3/2
Se per esempio un corpo cade da una altezza di 100 m abbiamo x = 1.53 cm.
Appendici
Somma vettoriale, prodotto vettoriale e prodotto scalare
Spesso per indicare una grandezza fisica è necessario uno spostamento ed anche una direzione in cui abbiamo
effettuato lo spostamento. L'unione di queste due informazioni prende il nome di vettore.
In queste pagine il vettore è indicato in grassetto mentre lo spostamento (chiamato modulo) si indica
con il carattere normale.
Per es. P è il vettore e P è il modulo.
In genere viene rappresentato con una freccia della quale la lunghezza è proporzionale allo spostamento mentre
la direzione vien data dall'orientamento.
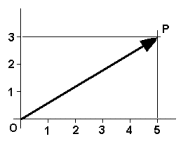 Per esempio nella figura vediamo un vettore relativo allo spostamento da O al punto P di coordinate (5,3).
Per esempio nella figura vediamo un vettore relativo allo spostamento da O al punto P di coordinate (5,3).
Il modulo di P si ottiene con il teorema di Pitagora:
P2 = 52 + 32 = 34 per cui, calcolando la radice quadrata, P = 5.83.
Si chiama somma vettoriale la somma di due, o più, vettori e si esegue con vari metodi, il più intuitivo è il
metodo grafico: si somma un vettore facendo coincidere la punta dell'uno in corrispondenza della coda dell'altro
detto anche regola del parallelogramma.
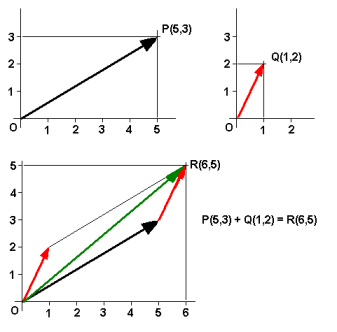 Dalla figura è chiaro anche che la somma si può ottenere sommando tra loro i valori (dette componenti) sugli assi cartesiani
R=(5+1,3+2)=R(6,5).
Dalla figura è chiaro anche che la somma si può ottenere sommando tra loro i valori (dette componenti) sugli assi cartesiani
R=(5+1,3+2)=R(6,5).
Analogamente alla somma si ottiene la differenza:
scrivere R = P - Q significa togliere Q
da P e quindi in componenti: R(5-1,3-2)=R(4,1) mentre col metodo grafico dovrei mettere il vettore rosso
capovolto, con la punta a posto della coda.
I prodotti scalare e vettoriale sono due "moltiplicazioni di vettori", la prima dà un numero (uno scalare appunto)
e si ottiene dalla relazione:
P · Q =PQ cos a
Dei vettori si usa solo il modulo mentre a è l'angolo che formano l'uno rispetto a l'altro.
Il prodotto vettoriale è dato dalla relazione:
P x Q = i (PQ sin a)
si ottiene un vettore i di modulo PQ sin a e orientato in direzione ortogonale al piano che contiene
P e Q.
torna su
Derivate
Quando dico: "Sto andando a 50 Km/h!" ho appena fatto una derivata senza accorgermene.
Se mi sposto con l'auto e vado da A a B in 1 ora e tra A e B ci sono 60 Km posso dire che ho viaggiato alla
velocità di 60 Km/h. Questa è la velocità media e non tiene conto se lungo il viaggio ho percorso
l'autostrada andando a 110 Km/h e poi sono uscito e mi sono ritrovato nel traffico cittadino andando a 40 Km/h al massimo.
Come so di essermi spostato a 110 Km/h? L'ho letto sul tachimetro naturalmente ma potevo anche guardare quanto tempo
impiegavo a fare 1 Km con un cronometro a velocità costante e risalire alla velocità con la relazione V=D/T dove V è la velocità,
D la distanza e T il tempo. Potevo misurare anche il tempo impiegato a fare 100 m o 10 m o pochi cm, dipende
solo dalla sensibilità del cronometro. Quindi nella relazione V=D/T posso mettere D e T piccoli a piacere e la
velocità V non cambia dato che l'ho supposta costante.
Se la velocità non è costante, diminuendo D e T posso conoscere la velocità istantanea che è quella misurata
dal tachimetro e che varia istante per istante.
Una derivata è solo una divisione di due valori molto piccoli o infinitesimi e, nel caso della velocità, posso scrivere
V=dD/dt dove dD è lo spostamento infinitesimo e dt il tempo infinitesimo.
Analogamente alla velocità posso scrivere l'accelerazione, che è la variazione della velocità nel tempo, come
a=dV/dt e per le proprietà delle derivate essendo V=dD/dt, ottengo: a=d(dD/dt)/dt=d2D/dt2.
torna su

 (la velocità angolare è la velocità alla quale ruota la giostra).
(la velocità angolare è la velocità alla quale ruota la giostra).
 Poiché g è la somma di go e l'accelerazione centrifuga, la direzione di g è chiamata
verticale ed è determinata dalla direzione del filo a piombo. I liquidi si dispongono con la superficie perpendicolare
a g. La direzione di g non punta perfettamente verso il centro della Terra (se supponiamo che sia
una sfera perfetta) ma è spostato in base alla accelerazione in quel punto.
Poiché g è la somma di go e l'accelerazione centrifuga, la direzione di g è chiamata
verticale ed è determinata dalla direzione del filo a piombo. I liquidi si dispongono con la superficie perpendicolare
a g. La direzione di g non punta perfettamente verso il centro della Terra (se supponiamo che sia
una sfera perfetta) ma è spostato in base alla accelerazione in quel punto. Per esempio nella figura vediamo un vettore relativo allo spostamento da O al punto P di coordinate (5,3).
Per esempio nella figura vediamo un vettore relativo allo spostamento da O al punto P di coordinate (5,3). Dalla figura è chiaro anche che la somma si può ottenere sommando tra loro i valori (dette componenti) sugli assi cartesiani
R=(5+1,3+2)=R(6,5).
Dalla figura è chiaro anche che la somma si può ottenere sommando tra loro i valori (dette componenti) sugli assi cartesiani
R=(5+1,3+2)=R(6,5).